Campo magnético
en un conductor recto
Para comprender de
una manera más fácil el campo magnético en
una bobina o solenoide, es importante estudiar el campo magnético que
genera una corriente eléctrica en un conductor recto.
Cuando se esparcen
limaduras de hierro sobre el papel y se atraviesa un conductor recto por el que
se hace pasar corriente eléctrica, se observa como las limaduras se alinean
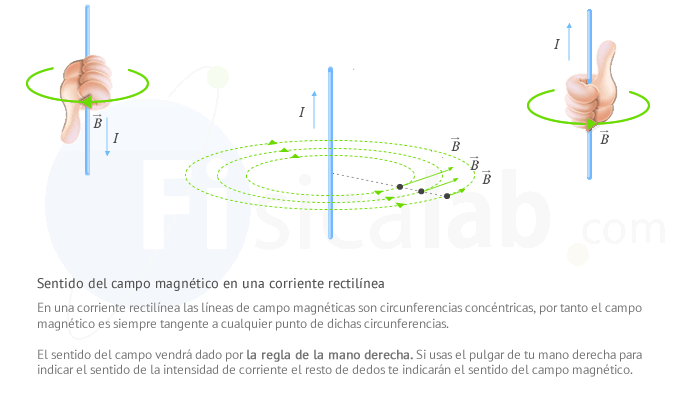
alrededor de conductor, tomando la forma de círculos concéntricos. Ampere ideo
una regla para determinar la dirección del campo que rodea un conductor recto denominada regla
de pulgar de la mano derecha.
La intensidad del
flujo magnético B, generada
por una corriente a través de un conductor, puede calcularse con la siguiente
expresión:
B= µI
2πr
Donde:
B= intensidad del
flujo magnético en teslas.
µ= Permeabilidad
del medio que rodea al conductor de Tm/A.
I= Intensidad de la
corriente que circula por el conductor de amperes.
R=Distancia perpendicular entre el conductor y un
punto determinado en metros.
Campo Magnético
producido por una espira
Una espira es
un hilo conductor en forma de línea cerrada, pudiendo ser circular,
rectangular, cuadrada, etc. y es una de las vueltas de una bobina.
Si por la espira hacemos circular
una corriente eléctrica, el campo magnético creado se hace más intenso en el
interior de ella.

Formula:
Donde:
B= intensidad de campo
magnético en Teslas (T).
µ=
permeabilidad del medio que rodea el conductor en Tm/A
I = intensidad de la corriente
que circula por el conductor en amperes (A).
r= radio de la espira en
metros (m).
Ejercicios:
1. Un profesor
le pide a un alumno que calcule la intensidad del campo magnético en el centro
de una espira de radio igual a 5 cm cuando circula por ella una corriente de 4
A. ¿Cuál es la intensidad de campo magnético en teslas?
I= 4 A
r= 5 cm
= 0.05 m
B=?
µo= 4π x 10-7 Tm/A
Sustitución y
resultado
B= (4π x 10-7 Tm/A) (4 A) / 2(0.05 m)
B= 5.026 x 10-5 T
2. Calcula la intensidad
del campo magnético de una espira de radio 7 cm al circular por ella una
corriente de 3 A.
Datos
I= 3 A
r= 7 cm = 0.07 m
B=?
B= (4π x 10-7 Tm/A)(3 A) / 2(0.07 m)
B= 2.692 x 10-5 T
Campo magnético producido por un solenoide
Existe un
conductor de numerosas aplicaciones, denominado solenoide. Se define como una
bobina de forma cilíndrica que cuenta con un hilo de material conductor
enrollado sobre sí, a fin de que, con el paso de la corriente eléctrica, se
genere un intenso campo electrónico. Cuando este campo magnético aparece,
comienza a operar como un imán; el campo magnético es comparable al de un imán recto.
Si las espiras están muy cercanas un solenoide las líneas de campo entran por un extremo, polo sur, y
salen por el otro, polo norte. Si la longitud del solenoide es mucho mayor que
su radio, las líneas que salen del extremo norte se extienden en una región
amplia antes de regresar al polo sur; por esta razón, en el exterior del
solenoide se presenta un campo magnético débil. Sin embargo, en el interior de
éste, el campo magnético es mucho más intenso y constante en todos los puntos.
La intensidad del
campo magnético en un solenoide se calcula mediante:

B= µNI/L
Donde:
B= intensidad del
campo magnético en teslas (T)
µ=
permeabilidad del medio que rodea al conductor en Tm/A
I= intensidad
de la corriente que circula por el conductor en ampere (A)
N= número de
vueltas
L= longitud de
solenoide en metros (m)
El solenoide
fue creado por André-Marie Ampere en 1822
Un solenoide es
cualquier dispositivo físico capaz de crear una zona de campo magnético
uniforme. Un ejemplo teórico es el de una bobina de hilo conductor aislado y
enrollado helicoidalmente, de longitud infinita. En ese caso ideal el campo
magnético sería uniforme en su interior y, como consecuencia, fuera sería nulo.
No hay comentarios:
Publicar un comentario